Deleterious alleles maintained by recurrent mutation.
          stable equilibrium(read as "q hat," where $q$= 0) reached
                when rate of replacement (by mutation)
                balances rate of removal (by selection).

       µ = frequency of new mutant alleles per locus per generation
           µ = 10^-6 : 1 in 1,000,000 gametes has new mutant 

            then  =  $\sqrt{⋯}$    [see derivation ]

        Ex.: For recessive lethal allele (s  = 1) with mutation rate of µ = 10^-6
               then  =   $\sqrt{⋯}$   =    $\sqrt{⋯}$ =  0.001
 

Mutational Genetic Load
    Lowered selection against deleterious allele increases frequency
        Does medical intervention increase frequency of heritable conditions?
            in Homo (e.g., diabetes, myopia)
    Eugenics: 1920s ~ 1960s social policy
            Modification of human condition by selective breeding
            'positive eugenics': encouraging people with "good genes" to breed
            'negative eugenics': discouraging people with "bad genes'' from breeding
                   e.g., immigration control, compulsory sterilization, and worse
                   [See: SJ Gould, "The Mismeasure of Man"]

       Would eugenics be efficient at reducing frequency of rare deleterious alleles and (or) genotypes?
            What proportion of 'deleterious alleles' occur in heterozygous carriers?

       (2pq) / 2q² = p/q  1/q    [ if  q << 1, then p 1 ; homozygotes have two deleterious alleles)

             for s = 1, ratio 1000 / 1 : most variant alleles in heterozygotes,
                                                    not subject to selection

Conclusion: if most mutations are rare (u < 0.001) & selectively disadvantageous ( s > 0.01)
                      recurrent mutation cannot maintain population variation at high levels observed:

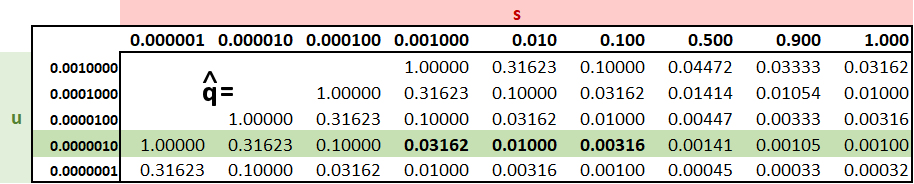
                       For u = 10^-6, is reciprocally proportional to s for s = 0.100 & 0.001
                                                  selection maintain> 0.03 iff s < 0.001

                                                                                       for paired values of s & µ 

HOMEWORK: Suppose presbyopia due to recessive allele p at a single locus, with mutation rate µ = 10^-5 from P p.
                               Suppose presbyopia is historically associated with selection coefficient s = 0.1,
                                   & vision correction has reduced selection by 90%.
                          1) What are the former vs new equilibrium frequencies of the p allele?
                         2) What are the former vs new equilibrium frequencies of persons with presbyopia ?
                         ^{3) EXTRA CREDIT: How many generations would it take to get there?}