Calculation of Variance: MOSSOM

For a series of number i = 1,2,...,n the arithmetic mean is calculated as

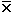        = (x_i) / n

And the variance (the mean squared deviation of each number from the sample mean) is calculated as

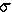         ² =  [ 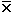- x_i]² / n

Modern PCs or hand-held calculators can calculate these values directly from the input series of numbers x_i. Mechanical desk calculators in use through the early 1970s required (1) entry and summation of x_i, (2) calculation of 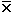, (3) re-entry of each x_i and calculation of the difference from 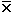, and (4) running summation of the square of the difference, a tedious calculation involving repeated re-entry of 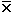. Early calculators simplify this slightly by storing 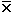in memory.

A more straightforward calculation recognizes that the variance is equal to the mean of squares, minus the square of means (mnemonic: MOSSOM), that is

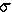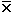         ² =  ( x_i² ) / n -   ²

In this form, the variance is calculated with two passes of the numerical series, one a summation of x to obtain the mean, and the second a summation of x².


In a simple example, the mean and variance of a series of four numbers 3, 1, 5, & 1 are

        (3 + 1 + 5 + 1) / 4   =   2.5

        [(2.5 - 3)² + (2.5 - 1)² + (2.5 - 5)² + (2.5 - 1)²] / 4 = 2.75

alternatively by the MOSSOM formula,

        (3² + 1² + 5² + 1²) /  4  - (2.5)²  = (36/4) - 6.25 = 2.75


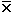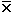Homework: Prove that [ - x_i]² / n = ( x_i² ) / n -   ²

---

All text material ©2017 by Steven M. Carr 

---