Genic Selection

AA	AB	BB
W₀	W₁	W₂
1	1 - s	(1-s)(1-s) = (1 - s)²

Genic Selection

In contrast to additive selection where each copy of the B allele modifies fitness by a constant amount s, in genic selection each copy of B modifies fitness by a constant factor (1- s). That is, fitness is multiplicative. Genic selection also models selection in populations of haploids, such as bacteria or viruses, because each deleterious allele in the population reduces population fitness by the same factor.

It can be shown that the change in allele frequencies in one generation of selection, where p = f(A), is

p' = (p) / (p + (1 - s)(q))

which re-written in terms of f(B) = q is

(1 - q') = ((1 - q) / (1 - q) + (1 - s)(q)) = (1 - q) / (1 - q + q - sq) = (1 - q) / (1 - sq)

-q' = (1 - q)/(1 - sq) - 1

q' = 1 - (1 - q)/(1 - sq) = - q / (1-sq)

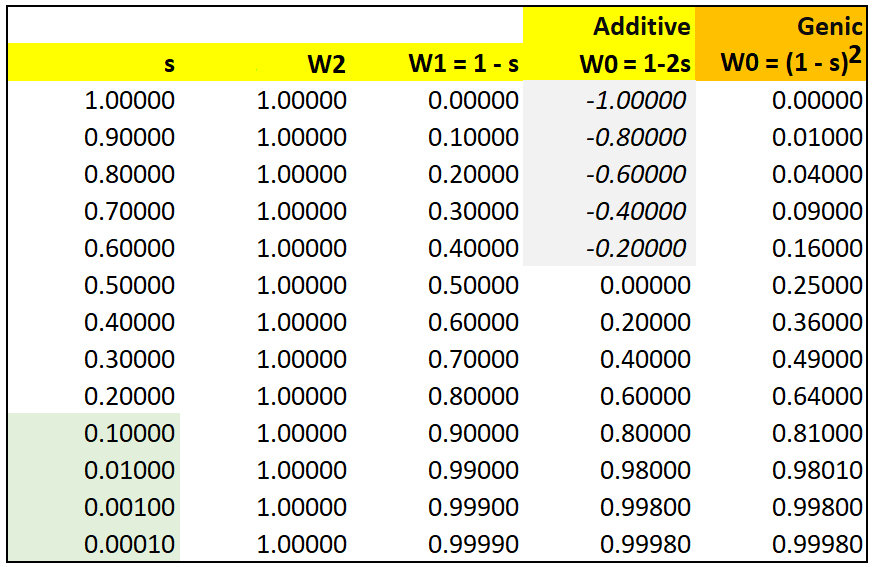
Unlike Additive selection, Genic selection can model large values of s, because the multiplicative contribution of alleles leaves a small but positive W2 fitness. Note that Genic selection converges on Additive selection when s < 0.01, because (1 - s)² = 1 - 2s + s² ~ (1 - 2s) when the s² term is negligible.

HOMEWORK: Use the GSM model in Excel to examine the shape of the curves for Additive, Genic, & Dominant selection against a deleterious recessive for the same values of s.