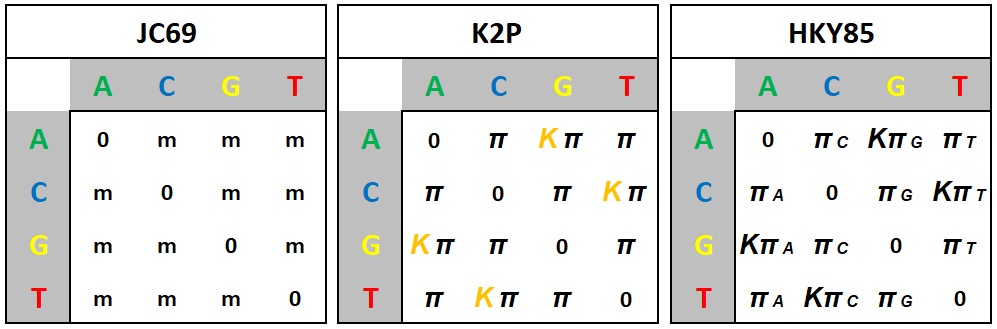
Models of Molecular Evolution

Models of Molecular Evolution
Given four
nucleotides A, C, G, & T,
there are (4x4) - 4 = 12 possible
pairwise mutations among them that result in a SNP.
Mutations rates among the four nucleotides can be set in various
ways, based on data and assumptions.
[Left] The
original and simplest model is the Jukes & Cantor (1969)
model, called JC69, which assumes that all nucleotide
frequencies are equal, and all mutations leading to a SNP
occur at the same rate, m. For example, the
reciprocal rates A ![]() C
and C
C
and C ![]() A are equal, and
equal to A
A are equal, and
equal to A
[Middle] A simple
adjustment is the Kimura Two-Parameter Model (K2P),
which
recognized from early DNA data that, at least in
comparisons within species and among closely-related species,
transitions (Ts) (A![]() [Ts] / [Tv]. As
sequence divergences increase, [Tv]
increases towards K
< 1, and Tv-only models may be more accurate.
[This occurs because Ts back
mutations (a
[Ts] / [Tv]. As
sequence divergences increase, [Tv]
increases towards K
< 1, and Tv-only models may be more accurate.
[This occurs because Ts back
mutations (a ![]() g
g ![]() a "flip-flops")
occur so rapidly that their current state between any two
sequences is uninformative. Slower Tv mutations then
provide more information].
a "flip-flops")
occur so rapidly that their current state between any two
sequences is uninformative. Slower Tv mutations then
provide more information].
[Right] Given the
availability of data and increased understanding of molecular
evolution, it became apparent that besides the Transition Bias,
nucleotide frequencies in either DNA strand are
unequal, and that mutation rates between nucleotide
pairs are unequal. The Hasegawa,
Kishino, & Yano (1985) model (HKY85)
incorporates all these factors. In the last column, for example,
the mutation rate of any nucleotide A, C, or G
to T is the same (![]() T is weighted by K as
in the previous mode. Every other column has the same
arrangement.
T is weighted by K as
in the previous mode. Every other column has the same
arrangement.
[Below] Advanced Methods: As
computational power and extensive data became available, it is
now possible to construct a universal model, called the
General Time Reversible (GTR) model, which allows
all available information to be incorporated into any particular
evolutionary investigation. Estimates of mutation rates are
calculated from the data themselves. In the last column, for
example,
![]() g
g ![]() a). The GTR was
previously prohibitively machine-time intensive, and remains so
if it has to be re-calculated for each bootstrap
replication. A heuristic solution is to use the same
estimated GTR matrix for all bootstraps.
a). The GTR was
previously prohibitively machine-time intensive, and remains so
if it has to be re-calculated for each bootstrap
replication. A heuristic solution is to use the same
estimated GTR matrix for all bootstraps.
where there are six distinct reciprocal
mutation rates: