Identity by Descent

Concept of Identity by Descent

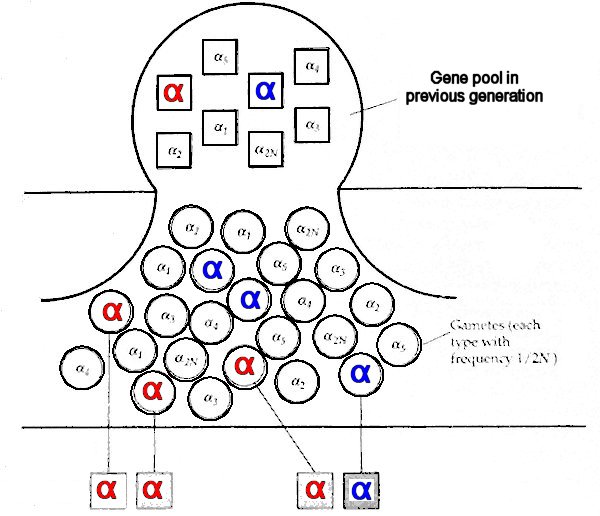
The gene pool of Generation i-1 comprises N individuals with a total 2N alleles, shown here as a, a, a₁, a₂, a₃, ... a_2N. Each allele produces a large number of daughter alleles in the gamete pool. We ask, what is the probability that two randomly chosen alleles will be Identical by Descent (IBD), that is, exact genetic copies of the same allele. This will occur if both alleles are copies of the same allele [aa] in the present generation, which has a probability of 1/(2N). Alternatively, if the alleles are copies of different alleles [aa], which has a probability of [1 - 1/(2N)], the two alleles will be IBD if they are descended from alleles that are IBD in the previous generation, with a probability of F_i-1.

Then the combined probability is

F_i = 1/(2N)[1] + (1 - 1/(2N))[F_i-1] Rearranging 1 - F_i = (1 - F_i-1)(1 - 1/(2N)) and the recursion equation back to the 0^th generation gives 1 - F_i = (1 - F₀)(1 - 1/(2N))^t

Since (1 - 1/(2N)) < 1, (1 - F_i) goes to zero and F goes to 1 at a rate proportional to the inverse of the population size. That is, all alleles in a finite population eventually become identical by descent from a single allele present in the original population: inbreeding is complete.