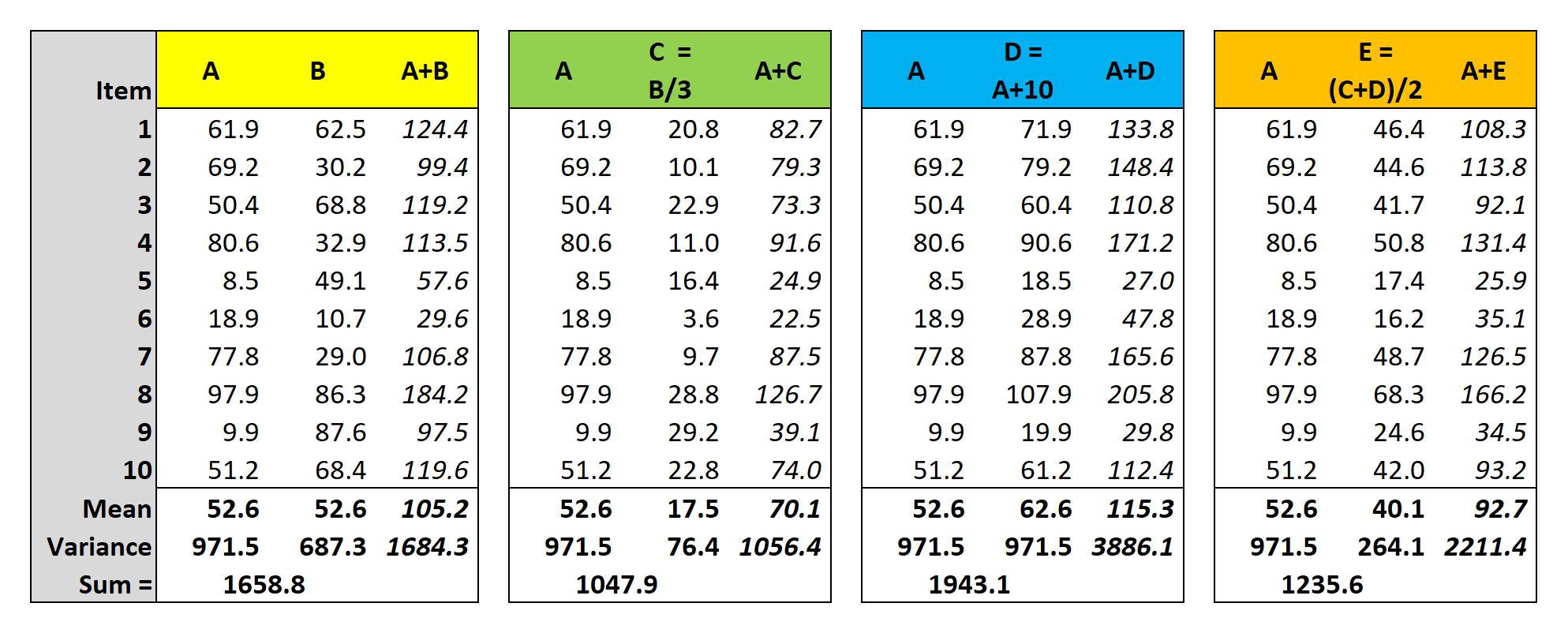
A demonstration of the Additivity of Variance
In the first block, two genetic loci A and B contribute to a combined
trait A+B. The
contributions of the two loci are (1) approximately equal
(means are similar) and (2) independent (A & B are not correlated).
Then, the phenotypic value
of the combined trait is simply the sum of the two
contributing loci, and the variance of (A+B) is the sum of the
variances of A & B separately. That is,
variance is additive.
In the second block, variance is not sensitive to moderate differences in the relative contribution of loci. C contributes only 25% of the value of the combined trait. Means and variances remain essentially additive (expected 1048 vs observed 1056). This is in part because locus A with a greater mean than locus B contributes more to the variance.
In the third block, variance is much more sensitive to non-independence of the contribution of loci. D simply adds 10 units to A: the variances of A and D are therefore identical. The variance of the combined trait is much greater than the sum of the contributing variances, because the two contributing loci are perfectly correlated.
In the fourth block, trait E has equal contributions from the transformed values of A & B in C & D in the second and third blocks. Because in D the A+10 contribution is still perfectly correlated with A, the variance of E is substantially greater than that of A + B
Additivity of variance is a crucial assumption of many biological experiments and analyses, especially Analysis of Variance (ANOVA) and estimation of Heritability. Non-additivity contributes to interaction variance, where a combined trait value cannot be predicted from measurements of the component traits.
In the second block, variance is not sensitive to moderate differences in the relative contribution of loci. C contributes only 25% of the value of the combined trait. Means and variances remain essentially additive (expected 1048 vs observed 1056). This is in part because locus A with a greater mean than locus B contributes more to the variance.
In the third block, variance is much more sensitive to non-independence of the contribution of loci. D simply adds 10 units to A: the variances of A and D are therefore identical. The variance of the combined trait is much greater than the sum of the contributing variances, because the two contributing loci are perfectly correlated.
In the fourth block, trait E has equal contributions from the transformed values of A & B in C & D in the second and third blocks. Because in D the A+10 contribution is still perfectly correlated with A, the variance of E is substantially greater than that of A + B
Additivity of variance is a crucial assumption of many biological experiments and analyses, especially Analysis of Variance (ANOVA) and estimation of Heritability. Non-additivity contributes to interaction variance, where a combined trait value cannot be predicted from measurements of the component traits.