Quadratic solution of the Migration / Selection
equilibrium
To solve  qi = tqi2 - (m + t)(qi) + mqm
qi = tqi2 - (m + t)(qi) + mqm
Recall the quadratic formula: 0
= [-b 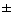
 (b2 - 4ac)] / 2a
(b2 - 4ac)] / 2a
Then, set terms of quadratic as a
= t b
= - (m + t) c
= mqm
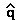 = [ (m + t)
= [ (m + t) 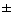
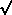 [( (-1)2(m + t)2
- 4tmqm]
] / 2t
quadratic form
[( (-1)2(m + t)2
- 4tmqm]
] / 2t
quadratic form
= [ (m + t) 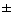
 [m2 + t2
+ 2mt - 4mt] ] / 2t
qm =
1; expand ( - (m + t) )2
[m2 + t2
+ 2mt - 4mt] ] / 2t
qm =
1; expand ( - (m + t) )2
 [ (m + t)
[ (m + t) 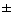
 [t2 +
2mt - 4mt] ] / 2t
if
m < t , then m2 << t2
[t2 +
2mt - 4mt] ] / 2t
if
m < t , then m2 << t2
 [
(m + t)
[
(m + t) 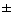
 [t2
+ (t2)(2m/t - 4m/t)] ] / 2t
create common t2 term
[t2
+ (t2)(2m/t - 4m/t)] ] / 2t
create common t2 term
 [
(m + t)
[
(m + t) 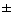 (t)
(t)  [1 + 2m/t - 4m / t] ] / 2t
factor out
[1 + 2m/t - 4m / t] ] / 2t
factor out 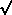 t2 term as t
t2 term as t
 [ (m + t)
[ (m + t) 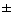 (t)(1
+ m/t - 2m/t) ] /
2t
apply approximation
(t)(1
+ m/t - 2m/t) ] /
2t
apply approximation
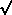 (1
(1 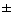 x)
x)  ( 1
( 1 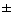 (x/2))
(x/2))
because (1 +
x/2)2 = 1 + x +
(x/4)2
 (1 + x) iff x << 1
(1 + x) iff x << 1
that is (- m / t) << 1
For which the negative root, if t >
0, is
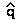

(m + t) - (t + m
- 2m) / 2t
t & m
terms cancel [ pretty !]
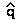
 2m / 2t = (m / t)
if qm
= 1 as in standard model, & m < t
2m / 2t = (m / t)
if qm
= 1 as in standard model, & m < t