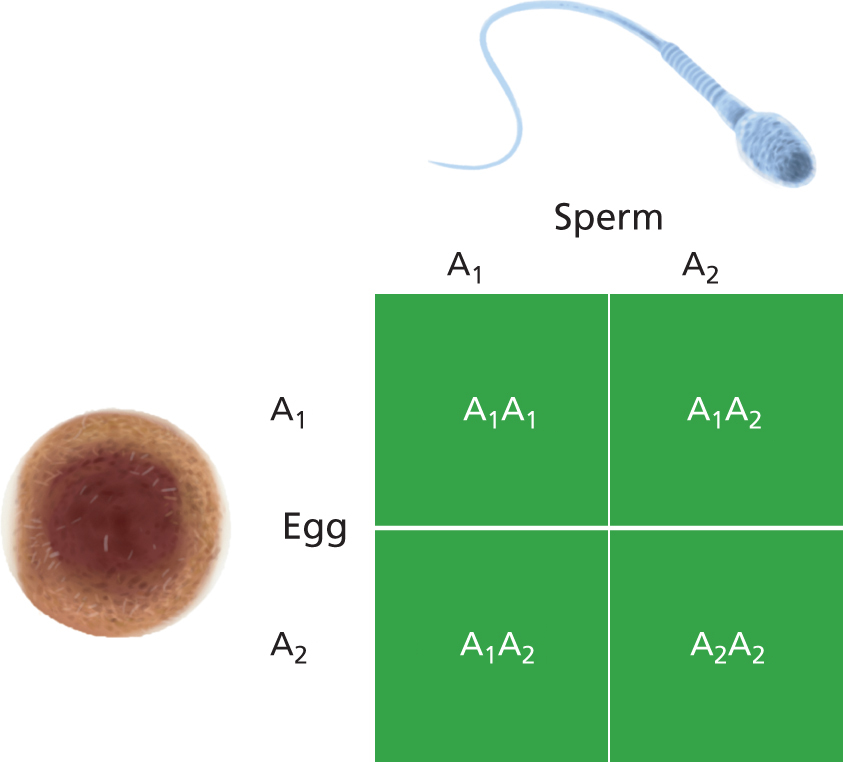
Recall that in Mendelian genetics, the Punnet Square [left] shows the results of a single cross between two Aa individuals, in which case the square is divided into four equal quarters, each representing 1/4 of the offspring.
Let frequency
of A allele f(A) = p
Let frequency of a
allele f(a) = q
Let allele
frequencies in males & females be equal (qm = qf).
What are the expected
genotype frequencies after one generation of random
union of gametes?
I. What are the probabilities of
obtaining various gametic combinations?
prob.
of
A from male & A from
female: pm x pf =
p2
prob.
of
a from male & a from
female: qm x qf
= q2
prob.
of
A from male & a from female,
or a from
male & A from female: (pm
x qf ) + (pf x qm ) = 2pq
II. What is the result of the binomial expansion of p & q in males & females ?
(pm + qm) (pf + qf) = p2 + 2pq + q2
III. What are the areas of the four boxes of a Punnet Square ?


Recall that in Mendelian genetics,
the Punnet Square [left] shows the results of a single
cross between two Aa individuals, in which case the
square is divided into four equal quarters, each representing
1/4 of the offspring.
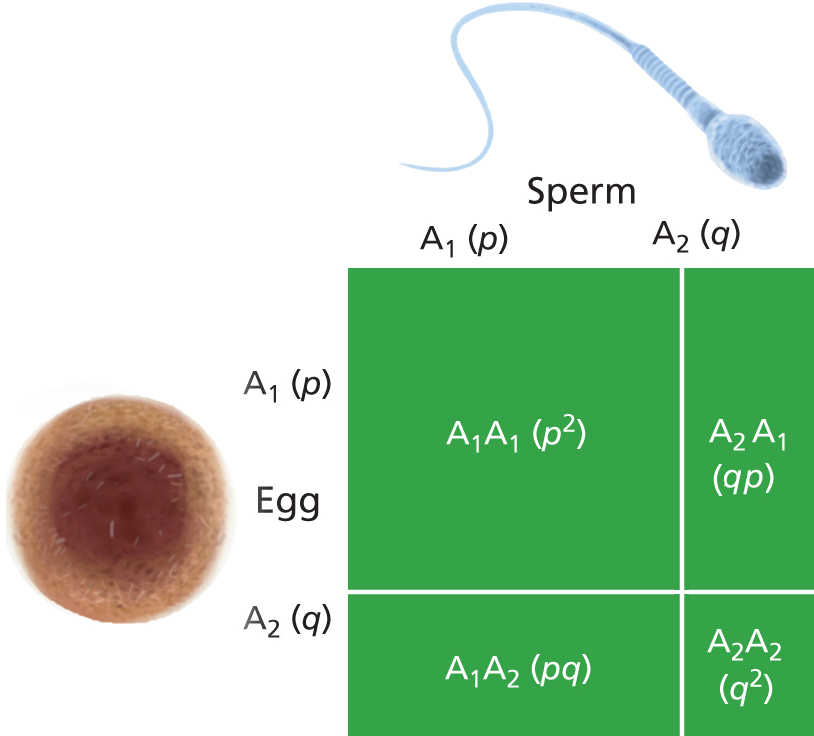
In a population of individuals with allele
frequencies p & q [right], the two axes are
divided as the relative proportions of p
& q in males and female gametes. Then, the areas of
AA, Aa, and aa are AA = p2, (pq +
pq) = 2pq,
and aa = q2.
By any of the three
methods: f(AA) = p2
f(Aa)
=
2pq f(aa) = q2