
Applications of Game Theory
to Evolutionary Biology
Mixed-strategy solutions for
2x2 games can be calculated
arithmetically. More complicated games with multiple
strategies require the use of matrix algebra: an
entertaining and enlightening book is JD Williams' "The
Compleat Strategyst" (2nd ed., 1966).
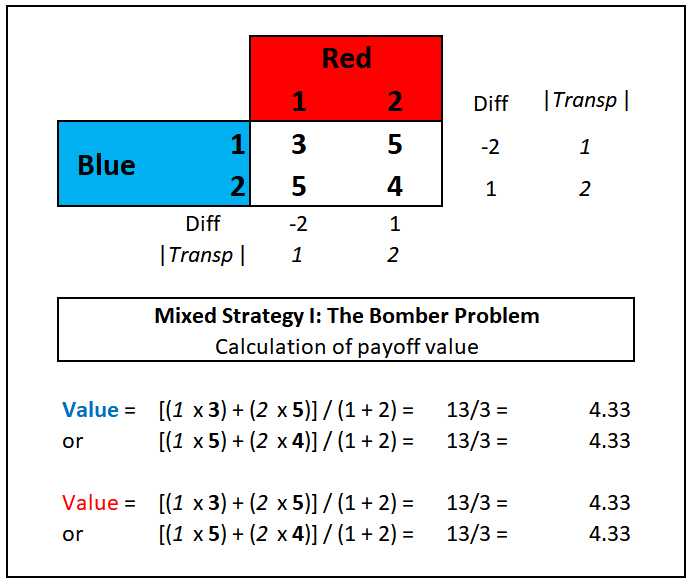
In the so-called "Bomber Defense Problem," Blue has two planes, one of which carries the bomb and the other of which carries protective equipment for defense & counter-measures, etc. The planes fly in in a formation that provides one with protection by the other: the bomber can fly in the unprotected (Blue 1) or protected (Blue 2) position, and the other plane in the other position. Red has a single fighter, which can attack either the unprotected (Red 1) or protected plane (Red 2), but not both. (This particular example was featured prominently by the RAND Corporation in initial discussions of Game Theory as applied to military situations).
Blue wins if the bomber gets through (100% success). Convert the probabilities of bomber success to payoffs to Blue, with p = 100% = 5). Blue will always win if the Red fighter attacks the wrong plane, in either position (prob 100%: payoff 5). Blue may win if the bomber is attacked in the unprotected (prob 60%: payoff 3) or protected (prob 80%: payoff 4) positions. The value of the game to Blue can be calculated as 4.33 (prove this to yourself). Compare this to what happens if both sides do what comes naturally: Blue always places the bomber in the protected position (Blue 2), and Red always attacks that position, assuming it to be the bomber (Red 2). The value of the game to Blue is exactly 4. The difference in the Value to Blue of adopting a mixed versus a pure strategy is (4.33 - 4.00) / 4.00 = 8.25%, which is a marked gain.
The value 4.33 is the minimax payoff, that is, both the minimum and maximum payoff, if Red also uses the optimal strategy. It is also the maximum value to Blue, if Blue plays any other strategy, and is the minimum value, if Red plays any other strategy.
HOMEWORK: Calculate the payoff if Blue uses the mixed strategy and Red always attacks the protected plane. Calculate the payoff, if Red attacks the protected and unprotected plane with equal frequency.
The "Attack-Defense problem" is applicable to within-species interactions subject to Natural Selection. For example, various species defend territories that include several resource types of differing values. Interference Competition occurs when con-specifics on adjacent territories actively interfere with their neighbors in an attempt to gain resources. Blue has nesting and feeding areas (the latter more valuable in non-breeding seasons), and can defend one or the other (Blue 1 & Blue 2) but not both. Red may attack either area (Red 1 & Red 2), but not both. Blue can defend successfully an attack on either area (payoff 3). A Red attack on an undefended nesting area is a minor loss to Blue (payoff -1), whereas a successful attack on an undefended feeding area is a major loss (payoff -9). The Value of a 3:1 mixed strategy for Blue is a break-even 0, compared with -1 for consistent defense of the more valuable resource at the cost of the less valuable: the gain to Blue is (3 - [-1]) / 3.00 = 1.33%, a modest gain. Note that this game is a 'zero-sum' game around an equilibrium, because gains and losses to the two con-specifics cancel.
If the payoff for a within-species interaction is a component of evolutionary Fitness, Game Theory predicts evolution of flexible optimal attack-defense behaviors, noting that single strategies are dis-favored by Natural Selection. Note as well that the relative values of the nesting and feeding areas will change seasonally, introducing another complexity into the game. Finally, games may become non-zero-sum games if the competing con-specifics place different values on resource areas. For example, a male may place zero value on a nesting area, and a value of 10 on a feeding area.
In the so-called "Bomber Defense Problem," Blue has two planes, one of which carries the bomb and the other of which carries protective equipment for defense & counter-measures, etc. The planes fly in in a formation that provides one with protection by the other: the bomber can fly in the unprotected (Blue 1) or protected (Blue 2) position, and the other plane in the other position. Red has a single fighter, which can attack either the unprotected (Red 1) or protected plane (Red 2), but not both. (This particular example was featured prominently by the RAND Corporation in initial discussions of Game Theory as applied to military situations).
Blue wins if the bomber gets through (100% success). Convert the probabilities of bomber success to payoffs to Blue, with p = 100% = 5). Blue will always win if the Red fighter attacks the wrong plane, in either position (prob 100%: payoff 5). Blue may win if the bomber is attacked in the unprotected (prob 60%: payoff 3) or protected (prob 80%: payoff 4) positions. The value of the game to Blue can be calculated as 4.33 (prove this to yourself). Compare this to what happens if both sides do what comes naturally: Blue always places the bomber in the protected position (Blue 2), and Red always attacks that position, assuming it to be the bomber (Red 2). The value of the game to Blue is exactly 4. The difference in the Value to Blue of adopting a mixed versus a pure strategy is (4.33 - 4.00) / 4.00 = 8.25%, which is a marked gain.
The value 4.33 is the minimax payoff, that is, both the minimum and maximum payoff, if Red also uses the optimal strategy. It is also the maximum value to Blue, if Blue plays any other strategy, and is the minimum value, if Red plays any other strategy.
HOMEWORK: Calculate the payoff if Blue uses the mixed strategy and Red always attacks the protected plane. Calculate the payoff, if Red attacks the protected and unprotected plane with equal frequency.
The "Attack-Defense problem" is applicable to within-species interactions subject to Natural Selection. For example, various species defend territories that include several resource types of differing values. Interference Competition occurs when con-specifics on adjacent territories actively interfere with their neighbors in an attempt to gain resources. Blue has nesting and feeding areas (the latter more valuable in non-breeding seasons), and can defend one or the other (Blue 1 & Blue 2) but not both. Red may attack either area (Red 1 & Red 2), but not both. Blue can defend successfully an attack on either area (payoff 3). A Red attack on an undefended nesting area is a minor loss to Blue (payoff -1), whereas a successful attack on an undefended feeding area is a major loss (payoff -9). The Value of a 3:1 mixed strategy for Blue is a break-even 0, compared with -1 for consistent defense of the more valuable resource at the cost of the less valuable: the gain to Blue is (3 - [-1]) / 3.00 = 1.33%, a modest gain. Note that this game is a 'zero-sum' game around an equilibrium, because gains and losses to the two con-specifics cancel.
If the payoff for a within-species interaction is a component of evolutionary Fitness, Game Theory predicts evolution of flexible optimal attack-defense behaviors, noting that single strategies are dis-favored by Natural Selection. Note as well that the relative values of the nesting and feeding areas will change seasonally, introducing another complexity into the game. Finally, games may become non-zero-sum games if the competing con-specifics place different values on resource areas. For example, a male may place zero value on a nesting area, and a value of 10 on a feeding area.
Examples after JD Williams (1966); Figure & Text material © 2024 by Steven M. Carr