Introduction to Game Theory (I)
Game theory
conceptualizes interactions as games between two
players, Red and
Blue, with a range of
strategies available
to either player. The outcome of any pairwise combination
of strategies is shown in a matrix.
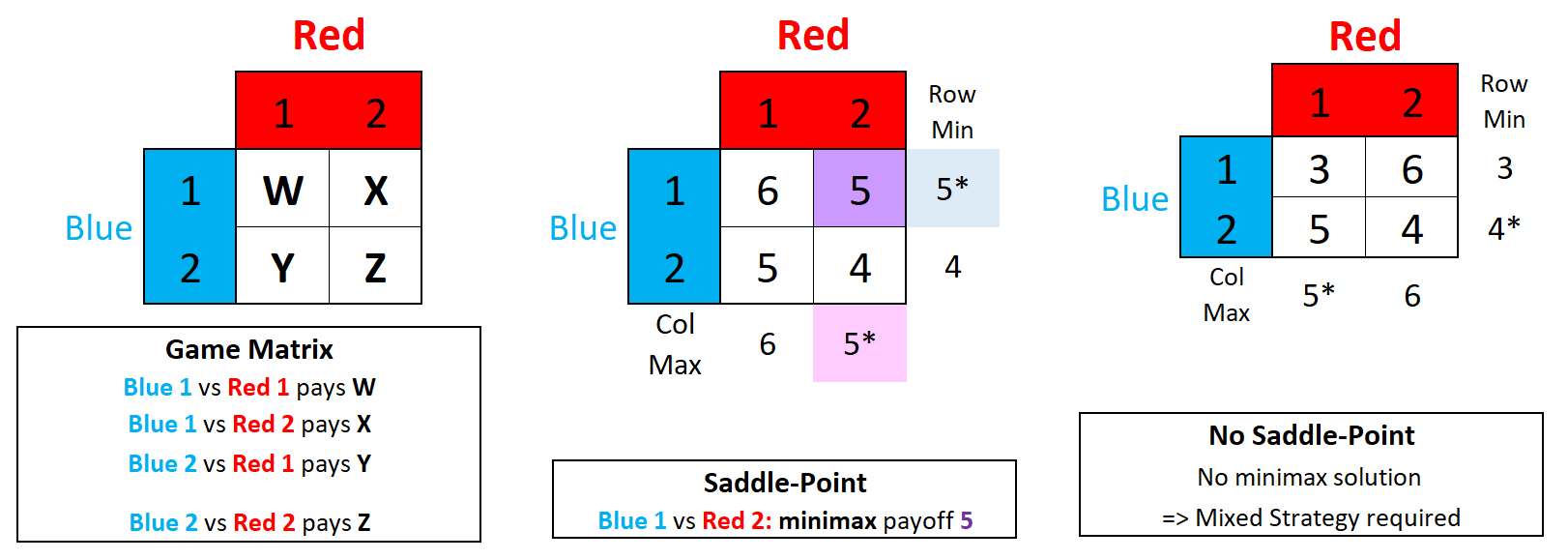
The simplest is a 2x2 game [left] in which each
player has two strategies, 1 & 2. The
matrix elements show the payoff to one player [Blue] of each pairwise
game. A positive value is a net gain for Blue, a negative value a
gain for Red. The
games shown here are called zero-sum: Blue gains equal Red
losses. The payoff matrices can be adjusted so that net
gains & losses are equal, or Blue can make a
side-payment to Red for
each play of the game. [A non-zero-sum game occurs
when the payoff matrices for the two players are different:
Blue and
Red place
different values on the outcome of any given
interaction].
Some games have a saddle-point [middle], in which one pair of strategies provides the maximum gain for Blue and the minimum loss for Red. This minimax point can be determined by finding the minimum gain for each row, and comparing this with the maximum loss for each column. If they are identical, the optimal outcome for either player is to play these two "pure" strategies consistently: any deviation guarantees a smaller gain for Blue or a greater loss for Red. In game theory, Blue 1 is said to 'dominate' Blue 2. Similarly, Red 2 dominates Red 1, remembering that Red is going for minimal loss. Then, Red 2 and Blue 1 intersect at minimax = 5.
Where a saddle-point does not exist [right], a combination of strategies (a "Mixed Strategy") is necessary for both players to obtain an optimum loss / gain for each. These games are more interesting.
Some games have a saddle-point [middle], in which one pair of strategies provides the maximum gain for Blue and the minimum loss for Red. This minimax point can be determined by finding the minimum gain for each row, and comparing this with the maximum loss for each column. If they are identical, the optimal outcome for either player is to play these two "pure" strategies consistently: any deviation guarantees a smaller gain for Blue or a greater loss for Red. In game theory, Blue 1 is said to 'dominate' Blue 2. Similarly, Red 2 dominates Red 1, remembering that Red is going for minimal loss. Then, Red 2 and Blue 1 intersect at minimax = 5.
Where a saddle-point does not exist [right], a combination of strategies (a "Mixed Strategy") is necessary for both players to obtain an optimum loss / gain for each. These games are more interesting.
Figure & Text material © 2024 by Steven M. Carr