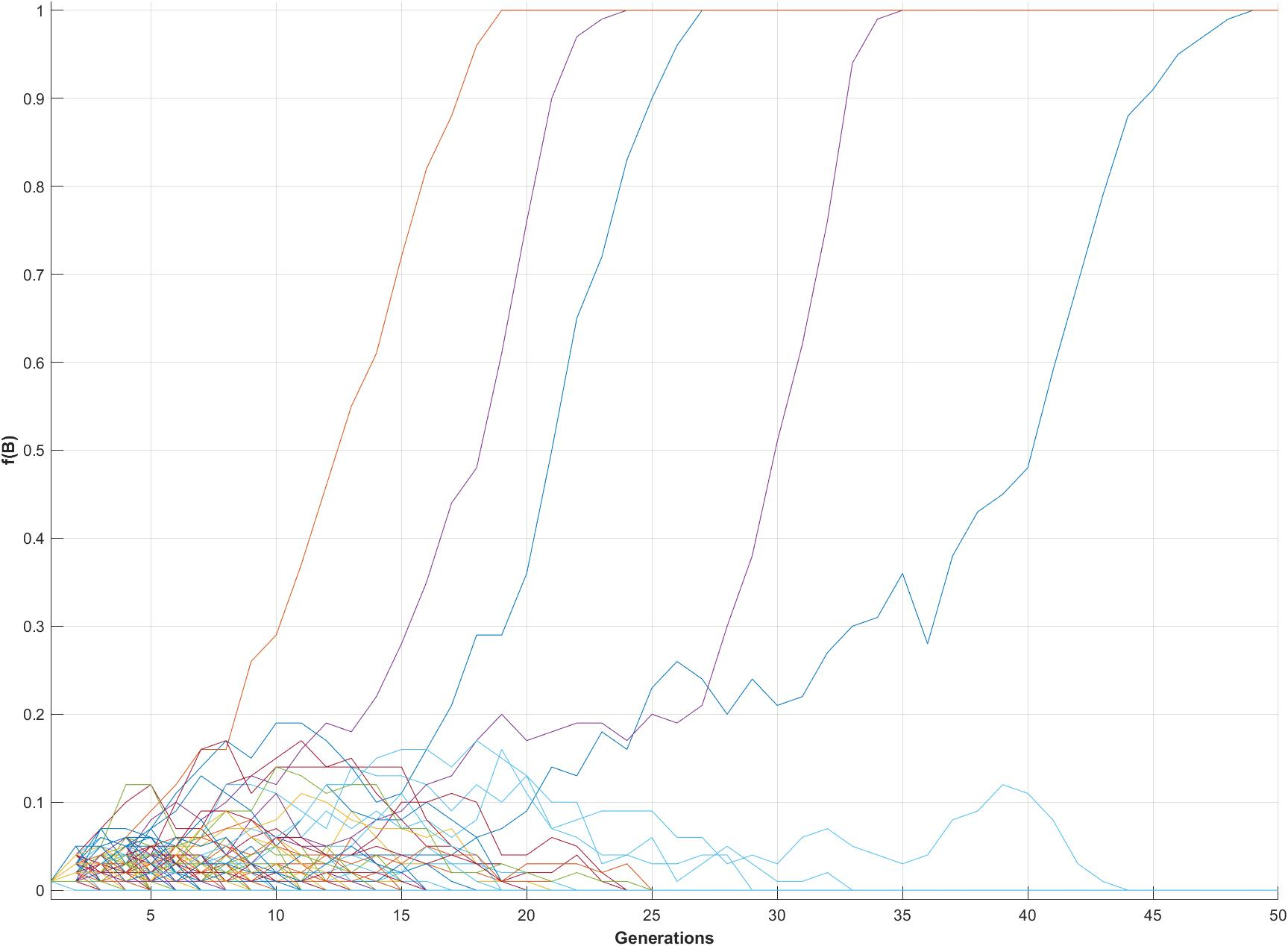
Fixation of a rare advantageous alleles: Modes of genetic speciation
(N = 50, q = 0.01; W0 = 0.5, W1 = 0.4, W2 = 1; 100 replicates)
Advantageous alleles arise occasionally in
a population by new mutation. Even with a major selective
advantage, most such variants never become common, and
disappear in a few generation. This is because a rare
advantageous recessive allele B rarely occurs in BB
genotypes, where the fitness advantage would make a
difference. Further, because a
single new mutant allele occurs at an initial f(B)
= 1/(2N), random loss by genetic
drift has greater influence than the selective
advantage. Depending on population size and the degree of
selective advantage, such an allele may drift to a critical
frequency, at which point the selective advantage drives it
rapidly to fixation.
In the example shown, among 100 replicate populations with N = 50, a single new variant occurs in a population at f(B)0 = (1)/(2)(50) = 0.01. The BB genotype has a two-fold selective advantage over AA. The new variant has lower fitness in heterozygous combination AB. In almost all replicates, f(B) 0. At f(B) ~ 0.2, f(BB) = 0.22 x 50 = 2, which means there is an expectation of two BB individuals in the population. The selective advantage of BB then allows f(B) to increase rapidly, in this case reaching fixation between t = 18 ~ 48 generations in five populations, while the variant in the other 95 populations has been lost.
One mode of allopatric speciation is peripatric speciation. A new allele that arises in a small founder population on the periphery of a large population may confer a novel local adaptive advantage. Such alleles are more likely to become 'fixed' in smaller populations than larger. This may occur in multiple small island populations separated from a mainland, as with honeycreepers on islands around New Guinea, where conditions on the islands different greatly from each other and from the mainland. Differential adaptation to islands in an archipelago may produce the same pattern: variable beak morphology in Darwin's Finches, or carapace shapes of Tortoises in the Galapagos Islands are examples.
HOMEWORK: Use the WriFish MatLab program to repeat the simulation above. Are the same results obtained every time? Is there a critical value of W2 with respect to W1 for routine fixation of ca. one population in a thousand (what is the ratio)? Is heterozygote disadvantage (W1 < W0 << W2) critical to the model (try W1 = 0.3, 0.4, & 0.5)? Adjust N and q to correspond to one variant in 5 or 500 individuals: can the same result be achieved?
In the example shown, among 100 replicate populations with N = 50, a single new variant occurs in a population at f(B)0 = (1)/(2)(50) = 0.01. The BB genotype has a two-fold selective advantage over AA. The new variant has lower fitness in heterozygous combination AB. In almost all replicates, f(B) 0. At f(B) ~ 0.2, f(BB) = 0.22 x 50 = 2, which means there is an expectation of two BB individuals in the population. The selective advantage of BB then allows f(B) to increase rapidly, in this case reaching fixation between t = 18 ~ 48 generations in five populations, while the variant in the other 95 populations has been lost.
One mode of allopatric speciation is peripatric speciation. A new allele that arises in a small founder population on the periphery of a large population may confer a novel local adaptive advantage. Such alleles are more likely to become 'fixed' in smaller populations than larger. This may occur in multiple small island populations separated from a mainland, as with honeycreepers on islands around New Guinea, where conditions on the islands different greatly from each other and from the mainland. Differential adaptation to islands in an archipelago may produce the same pattern: variable beak morphology in Darwin's Finches, or carapace shapes of Tortoises in the Galapagos Islands are examples.
HOMEWORK: Use the WriFish MatLab program to repeat the simulation above. Are the same results obtained every time? Is there a critical value of W2 with respect to W1 for routine fixation of ca. one population in a thousand (what is the ratio)? Is heterozygote disadvantage (W1 < W0 << W2) critical to the model (try W1 = 0.3, 0.4, & 0.5)? Adjust N and q to correspond to one variant in 5 or 500 individuals: can the same result be achieved?
Figure & Text material © 2025 by Steven M. Carr