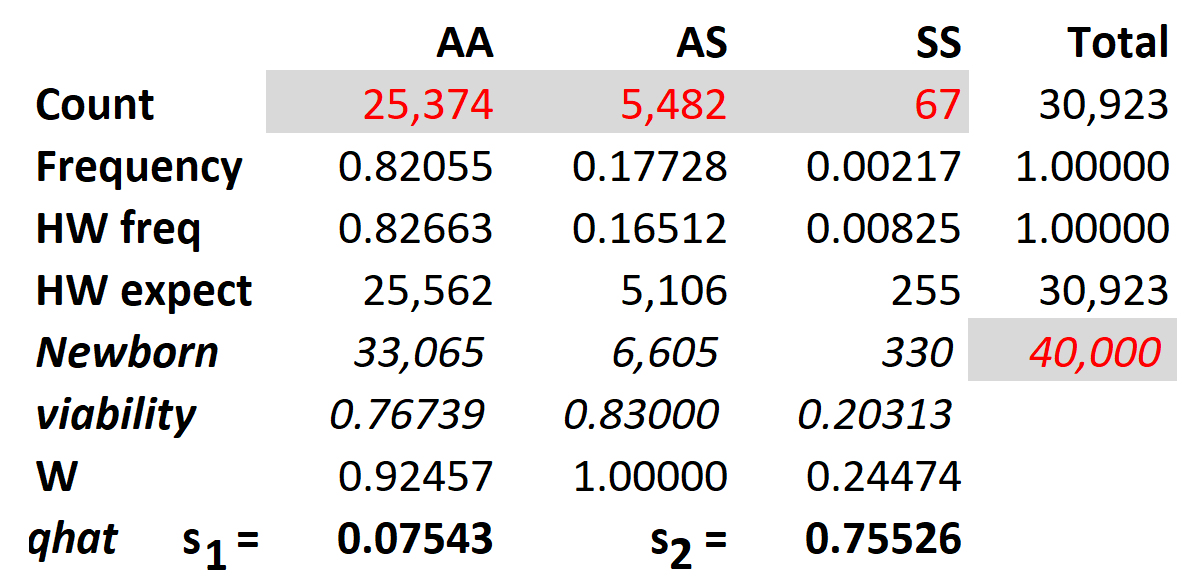
Estimation of selection
coefficients for the HbS allele
The data above, from the
early 1950s, record the numbers of persons in an African
population with Standard, Trait, and Sickle-Cell
phenotypes with respect to their AA AS,
and SS genotypes. These data allow calculation of
the relative Fitness values of the three
phenotypes, the selection coefficients
(s1 and s2)
of the SS and AA genotypes,
and equilibrium frequency of S.
From the observed counts, their observed frequencies are easily calculated. The observed q = f(S) = ( f(SS) + (0.5)f(AS) ), and the expected genotypes frequencies for Hardy-Weinberg expectations are then (1 - q)2, (2)(1-q)(q), & q2, as usual. Expected genotype counts are easily calculated.
These calculations apply to an adult population already subject to selective loss from malaria and sickle-cell disease. To compare these expected numbers to those of newborns not yet subject to selection, choose an arbitrary total number of newborns, greater than the total count of adults. [PROVE that the exact number does not make a difference. Why?]. Estimate the expected counts among newborns by multiplying this total by the Hardy-Weinberg expectations, e.g., 0.00825 x 40,000 = 330.
The relative viability (V) of each phenotype is the (Adult / Newborn) count. The Fitness (W) estimates of the AA & SS homozygotes relative to the AS heterozygotes are WAA = VAA / VAS and WSS = VSS / VAS , respectively, and the selection coefficients are then s1 = 1 - WAA and s2 = 1 - WSS, respectively
HOMEWORK:
1) Compare the observed & expected counts in the data above by Chi-Square. Explain the departure in terms of the relative numbers of each phenotype observed and expected, from your knowledge of sickle-cell disease.
2) A recent survey of 56,000 hospitalized patients in one middle eastern country identified 1,120 with sickle-cell disease (SS) and 13,440 with sickle-cell trait (AS). From these numbers and the formulae above, calculate the table values and estimate the selection coefficients against AA and SS. Test by Chi-square whether the adult population shows expected Hardy-Weinberg proportions.
3) Box 7.7 from Nielsen & Slatkin 2013 [below] includes a mis-calculation that leads to several errors in the results. Compare that calculation with the one below: what is the probable cause of the error? How could it be prevented?
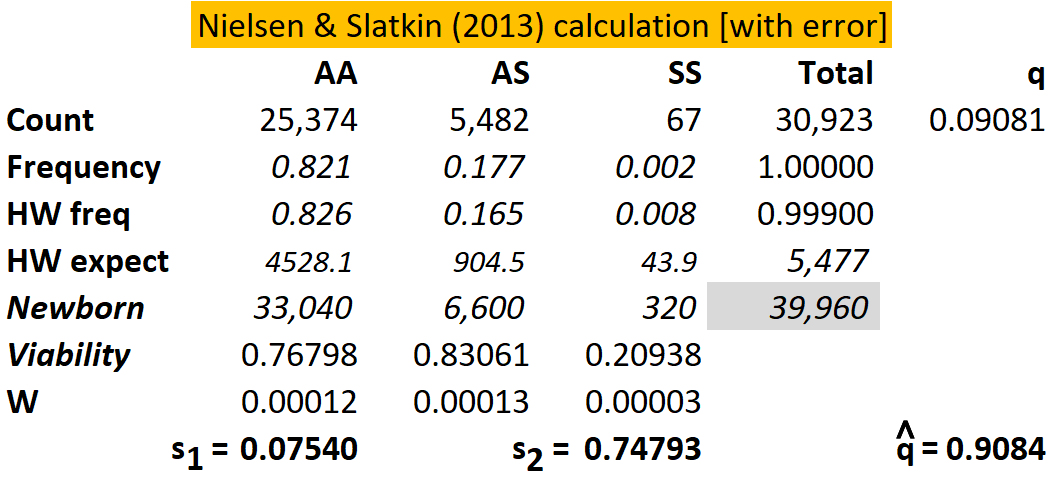
From the observed counts, their observed frequencies are easily calculated. The observed q = f(S) = ( f(SS) + (0.5)f(AS) ), and the expected genotypes frequencies for Hardy-Weinberg expectations are then (1 - q)2, (2)(1-q)(q), & q2, as usual. Expected genotype counts are easily calculated.
These calculations apply to an adult population already subject to selective loss from malaria and sickle-cell disease. To compare these expected numbers to those of newborns not yet subject to selection, choose an arbitrary total number of newborns, greater than the total count of adults. [PROVE that the exact number does not make a difference. Why?]. Estimate the expected counts among newborns by multiplying this total by the Hardy-Weinberg expectations, e.g., 0.00825 x 40,000 = 330.
The relative viability (V) of each phenotype is the (Adult / Newborn) count. The Fitness (W) estimates of the AA & SS homozygotes relative to the AS heterozygotes are WAA = VAA / VAS and WSS = VSS / VAS , respectively, and the selection coefficients are then s1 = 1 - WAA and s2 = 1 - WSS, respectively
HOMEWORK:
1) Compare the observed & expected counts in the data above by Chi-Square. Explain the departure in terms of the relative numbers of each phenotype observed and expected, from your knowledge of sickle-cell disease.
2) A recent survey of 56,000 hospitalized patients in one middle eastern country identified 1,120 with sickle-cell disease (SS) and 13,440 with sickle-cell trait (AS). From these numbers and the formulae above, calculate the table values and estimate the selection coefficients against AA and SS. Test by Chi-square whether the adult population shows expected Hardy-Weinberg proportions.
3) Box 7.7 from Nielsen & Slatkin 2013 [below] includes a mis-calculation that leads to several errors in the results. Compare that calculation with the one below: what is the probable cause of the error? How could it be prevented?

Figure © 2013 by Sinauer; Text material © 2020 by Steven M. Carr