Principles of Population Genetics
Various aspects of "Population"
gene pool (a genetic
unit):
all
the
alleles at a (single) locus
deme (an ecological unit):
all
the
conspecific individuals in an area
panmictic
unit
(a reproductive unit):
a
group
of randomly interbreeding individuals
sample (a numerical
unit):
a statistical subset of size 'N'
Theory of allele
frequencies: p's & q's
Genetic variation in populations can
be described by genotype and allele frequencies.
(not
"gene"
frequencies)
Consider a diploid autosomal
locus with two alleles and no dominance
(=>
semi-dominance: AA , Aa , aa
phenotypes are distinguishable)
# AA
= x # Aa = y # aa
= z x + y + z = N
(sample size)
f(AA) = x / N f(Aa)
= y / N f(aa) = z /
N
f(A)
= (2x + y) /
2N f(a)
= (2z + y) / 2N
or f(A) = f(AA) +
1/2 f(Aa) f(a) = f(aa) + 1/2
f(Aa)
let p = f(A), q = f(a)
p & q are allele
frequencies
Properties of p & q
p + q = 1 p = 1
- q q = 1 - p
(p
+
q)2 = p2 + 2pq + q2
= 1
(1
-
q)2 + 2(1 - q)(q) + q2 = 1
p & q are interchangeable wrt [read, "with respect to"]
A & a;
q is usually used for the
rarer,
recessive,
or deleterious (disadvantageous) allele;
BUT 'common'
& 'rare' are statistical properties
'dominant' & 'recessive' are
genotypic properties
'advantageous' & 'deleterious'
are phenotypic properties
*** combination of these properties is
possible ***
The
Hardy-Weinberg Theorem
What happens to p & q in
one generation of random mating?
Consider a population of monoecious organisms reproducing
by random union of
gametes
("tide pool" model)...
(1)
Determine the expectations
of
parental
alleles coming together in various genotype combinations.
[expectation: the
anticipated value of a variable  probability]
probability]
The probability
, binomial
expansion , Punnet
Square methods
all
show
that expectation of f(AA) = p2
expectation
of
f(Aa) = 2pq
expectation
of
f(aa) = q2
(2)
Re-describe allele frequencies among offspring (A' &
a').
f(A') = f(AA) + 1/2 f(Aa)
= p2 + (1/2)(2pq) = p2 + pq
= p(p+q) = p' = p
f(a') = f(aa) + 1/2 f(Aa)
= q2 + (1/2)(2pq) = q2 + pq
= q(p+q) = q' = q
The Hardy -
Weinberg Theorem (1908):
In the absence of other genetic or evolutionary
factors,
allele frequencies are invariant between generations, and
constant
genotype
frequencies are reached in one generation.
p2 : 2pq : q2 are Hardy-Weinberg proportions
(cf. Mendelian ratios 1 : 2 : 1 )
The
Hardy-Weinberg Theorem holds under "more realistic" conditions:
(1) multiple alleles /
locus
p
+
q + r = 1
(p
+
q + r)2 = p2 + 2pq + q2 + 2qr
+ r2 + 2pr = 1
The
proportion
of heterozygotes (H = 'heterozygosity')
is
a
measure of genetic variation at a locus.
Hobs = f(Aa) = observed heterozygosity
Hexp = 2pq = expected heterozygosity (for two
alleles)
He = 2pq + 2pr + 2qr = 1 - (p2 + q2
+ r2) for three alleles
n
He = 1 -  (qi)2 for n alleles
(qi)2 for n alleles
i=1
where qi = freq. of ith allele of n
alleles at a locus
Ex.: if q1 = 0.5, q2 = 0.3, & q3
= 0.2
then He = 1 - (0.52 + 0.32
+ 0.22) = 0.62
(2) sex-linked loci
iff [read: "if and only
if"] allele frequencies in males and females are identical
If
frequencies
are initially unequal, they converge
over several generations.
(3) dioecious organisms
sexes
are
separate
H-W
is
produced by random mating of individuals (random
union of genotypes).
expand (p2 'AA' + 2pq 'AB' + q2
'BB')2 :
nine possible 'matings' among genotypes
(See derivation)
No selfing
(self-fertilization not possible)
Application of Hardy-Weinberg to population
biology
Genotype proportions in natural
populations can be tested for H-W conditions
Ho(null hypothesis): no outside
factors are acting.
Ex.: MN blood groups in Homo
Among
North American whites:
|
MM
|
MN
|
NN
|
Sum
|
|
1787
|
3039
|
1303
|
6129
|
f(M) = [(2)(1787) + 3039] / (2)(6129)= 0.539
f(N) = [(2)(1303) + 3039] / (2)(6129)= 0.461
= 1.0 - 0.539
Chi-square ( 2) test:
2) test:
| |
#
|
expected
|
observed
|
(obs-exp)
|
d2/exp
|
|
MM
|
(0.539)2(6129)
|
1781
|
1787
|
6
|
0.020
|
|
MN
|
(2)(0.539)(0.461)(6129)
|
3046
|
3039
|
-7
|
0.012
|
|
NN
|
(0.461)2(6129)
|
1302
|
1303
|
1
|
0.000
|
|
|
|
|
|
 2 = 2 =
|
0.032ns
|
(cf. critical value p.05[1
d.f.] = 3.84)
(
p
>> 0.05)
note: there is only one degree of
freedom, because there are only two alleles
But
(you ask) won't "expected" always more or less equal "observed",
cuz
that's
where "expected" comes from?
Consider
an
artificial data set :
| |
MM
|
MN
|
NN
|
Sum
|
f(M)
|
f(N)
|
|
Navajo (US)
|
305
|
52
|
4
|
361
|
0.92
|
0.08
|
|
Koori (Aus.)
|
22
|
216
|
492
|
730
|
0.18
|
0.82
|
|
Combined
|
327
|
268
|
496
|
1091
|
0.42
|
0.58
|
(Homework: show that Navajo &
Koori populations exhibit H-W proportions)
Chi-square test on combined data:
| |
exp
|
obs
|
d=(o-e)
|
d2/exp
|
|
MM
|
192
|
327
|
135
|
94.9
|
|
MN
|
532
|
268
|
-264
|
131.0
|
|
NN
|
367
|
496
|
129
|
45.3
|
| |
|
|
 2 = 2 =
|
271.2**
|
(p
<<
0.01)
*=> A mixture of populations, each of which shows
Hardy-Weinberg proportions,
will not show expected Hardy-Weinberg proportions
if the allele frequencies are different in the separate
populations.
Wahlund Effect: an
artificial mixture of populations will have a deficiency
of heterozygotes
Evolutionary Genetics:
modification of Hardy-Weinberg
conditions
The Hardy-Weinberg conditions are
the 'null hypothesis':
What
are the consequences of other genetic / evolutionary phenomena?
Five
major factors:
1. Natural
selection
Change
of
allele frequencies ( q) [read as 'delta q']
q) [read as 'delta q']
occurs
due
to differential effects of alleles on 'fitness'
Consequences
depend
on dominance of fitness
(see Lab #1)
Natural
Selection
is the principle concern of evolutionary theory
(& first half of this course)
2. Mutation
A and A' are inter-converted at some rate µ .
If µ(A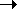 A')
A')  µ'(A
µ'(A A'), net change
will occur in one direction.
A'), net change
will occur in one direction.
3. Gene flow
Net
movement
of alleles between populations occurs at some rate m .
(Im)migration
introduces new alleles, changes frequency of existing alleles.
4. Population structure
Inbreeding: preferential
mating of relatives at some rate F
(see Homework).
Non-random reproduction:
variable sex ratio, offspring number, population size
5. Statistical sampling error
Chance
fluctuations
occur in finite populations, especially those with small
size N.
Genetic drift: random
change of allele frequencies
over
time
& among populations (see Homework)
All text
material © 2010 by Steven M. Carr
