Quadratic solution of the migration equation

---

To solve q_i  = tq_i² - (m + t)q_i + mq_m

Recall the quadratic formula: 0 = [-b 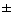(b² - 4ac)] / 2a
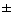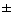        & note that, if x << 1, then  (1x)   1  (x/2)
                                            since   (1 + y/2)²  =  1 + y + (y/4)²    (1 + y)     if y << 1

Then, if m << t    and   a = t    b = -(m+t)   c = mq_m

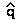
      (m + t) 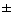[m² + t² + 2mt - 4mtq_m] / 2t

          (m + t) 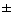[t² + t²(2m/t - 4mq_m/t)] / 2t

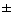          (m + t)  s[1 + 2m/t - 4mq_m/t] / 2t

          (m + t) 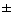 t[1 + m/t - 2mq_m/t] / 2t

For which the negative root, if  t > 0, is

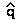
      (m + t) - [t + m - 2mq_m] / 2t

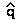
      2mq_m / 2t  =  (m / t)(q_m)

---

Text material © 2004 by Steven M. Carr

---